For When You Absolutely Need a Bigger Stack Than RAM Allows

Recently, I found an interesting programming exercise, which read:

“A robot is located at the bottom-left corner of a 5×5 grid. The robot can move either up, down, left, or right, but can not visit the same spot twice. The robot is trying to reach the top-right corner of the grid.”

In a series of blog posts we’ve managed to solve this simply and reasonably quickly whilst demonstrating the process of going from problem to solution. However, we cannot say we’ve done this very efficiently. Shredding through MB of memory in order to complete calculations like this one above meant we tired quickly of the OutOfMemoryException when attempting this for grids larger than 6×6. To help put this in perspective, that’s only 36 squares! It shouldn’t be so difficult.

The method in a nutshell: The paths being taken were stored on a Stack and at each juncture where, for the next step, there was more than one square to choose from a path was added to the stack for each after the current path had been removed from the stack. See, is this why few bother with pseudo-code. Thankfully, nobody’s reading this so no clearer explanation is necessary.

Having worked out that some kind of database is required and having ruled out a relational database we turn to Redis, an open source, advanced key-value store. The best part is that apart from being lightening fast it implements a stack. Perfect!

Whilst we’re adding code to use Redis stack functionality we’re interested in being able to preserve and swap out the different stack implementations: Memory, SQL Server & Redis. To do this we abstract towards an interface:

The IStack of T is introduced to allow List and List to be used indiscriminately for journeys as we’ve not settled on a representation for our disk based stack. The implementation for each of the three now looks like this:

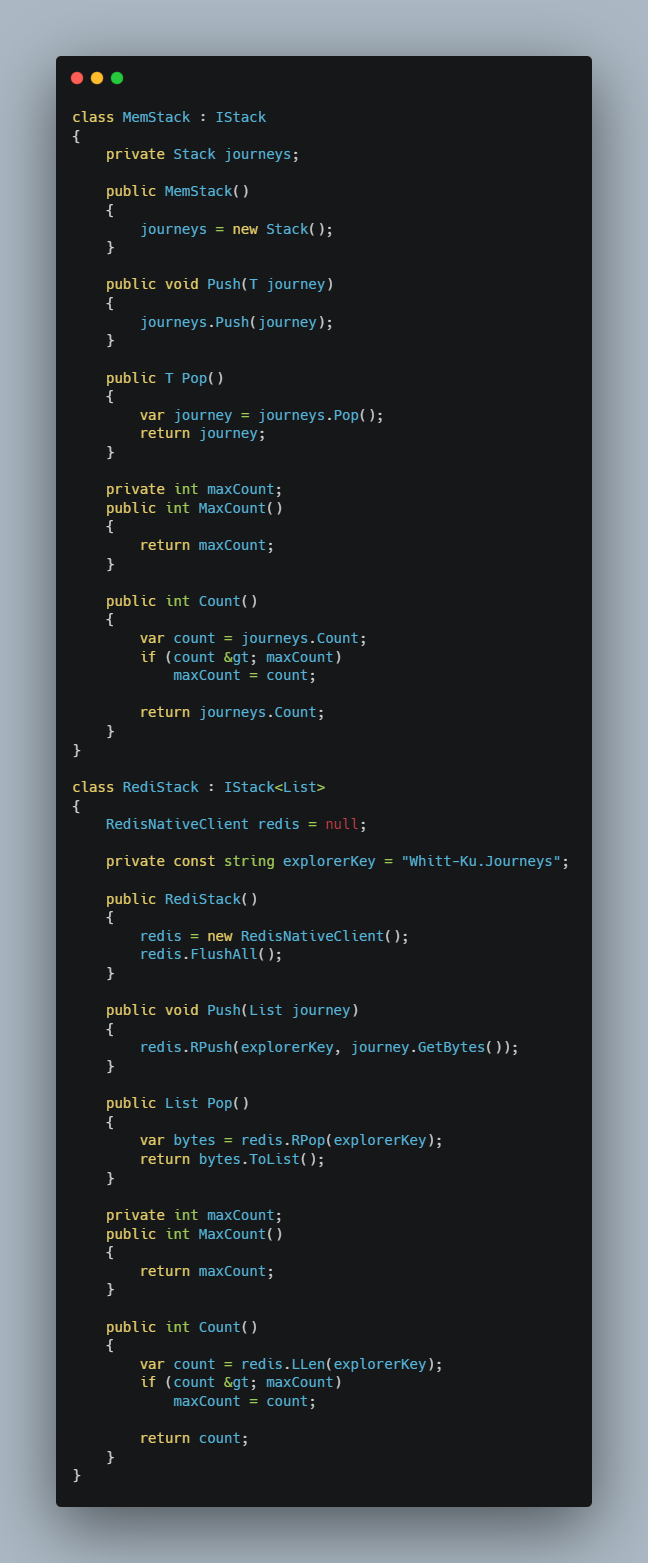
The RedisNativeClient is in fact a class within the ServiceStack.Redis library. It’s an “Open Source C# Redis client based on Miguel de Icaza previous efforts with redis-sharp.” We change the program for the last time:

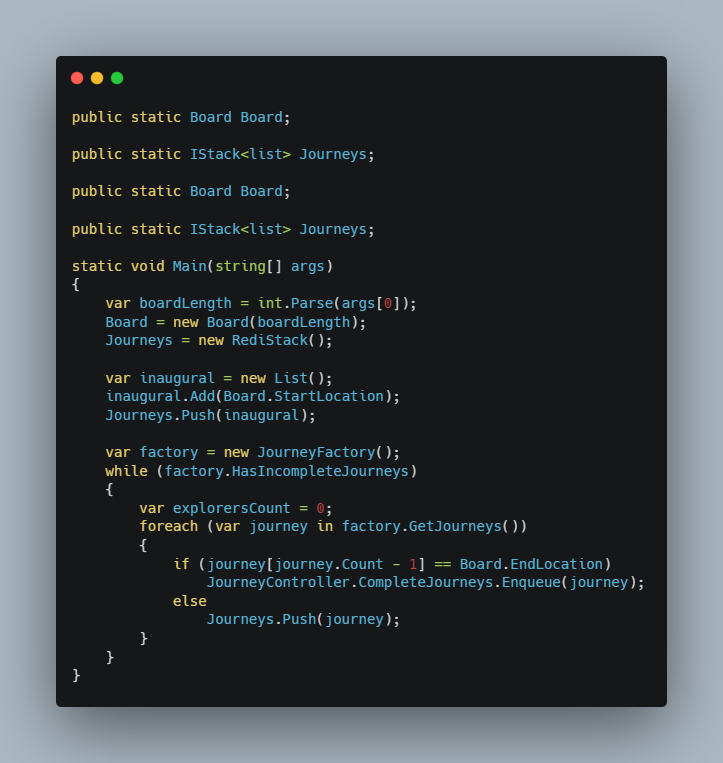
We run this with fingers crossed for a 5×5 grid and find that it’s ~70x slower than using RAM:

There are 8,512 unique paths from the top-left corner to the bottom-right corner of a 5x5 grid!
There were 90,110 robots used to discover this!
    Max stack: 16
    Total memory: 3,740,864
    Time elapsed: 18,538ms
    Garbage collection gen0: 701
    Garbage collection gen1: 10
    Garbage collection gen2: 0

The most recent results using RAM and List Generics implementation:

There are 8,512 unique paths from the top-left corner to the bottom-right corner of a 5x5 grid!
There were 90,110 robots used to discover this!
    Max stack: 16
Total memory: 2,704,944
Time elapsed: 256ms
Garbage collection gen0: 25
Garbage collection gen1: 6
Garbage collection gen2: 0

The reason why the same implementation using List was never used as the approach for Redis is shown below:

There are 8,512 unique paths from the top-left corner to the bottom-right corner of a 5x5 grid!
There were 90,110 robots used to discover this!
    Max stack: 16
Total memory: 3,798,576
Time elapsed: 1,302ms
Garbage collection gen0: 49
Garbage collection gen1: 4
Garbage collection gen2: 0

The code responsible for converting List to List has terrible performance so a binary representation of List is used instead as the value stored in Redis.

Finally, with little more performance to squeeze out using the current architecture we invite you to use this let us know how many unique paths there are on a 10×10 grid. Thanks.